Les Mathématiques au Quotidien

A quoi servent les mathématiques ?
Comme nous l'indique le dictionnaire Larousse, les mathématiques sont abstraites.
Il existe en effet de nombreux recueils/manuels remplis de formules réservés aux "matheux".
Pourtant, la connaissance de quelques règles de calcul simples, basées sur les quatre opérations
arithmétiques (l'addition, la soustraction, la multiplication et la division), est amplement suffisante
pour nous être utile dans notre quotidien avec une simple calculatrice et un tableur de type Excel.
Sans qu'il n'y paraisse, les Mathématiques sont en effet omniprésentes dans notre environnement.
Objectifs
L'approche proposée ici est extra-scolaire. Elle ne consiste donc pas à offrir une alternative aux manuels scolaires, ni même à vulgariser des concepts théoriques.
Il s'agit au contraire de découvrir les mathématiques au travers de ses applications possibles dans notre quotidien de façon à :
- Consolider les notions apprises à partir de la 6ème jusqu'en première, avec des exemples concrets d'applications des mathématiques dans différents domaines, notamment dans l'informatique et en physique.
- Se familisariser avec les informations chiffrées du quotidien (TVA, PIB, INSEE, pourcentages, proportions, systèmes d'unités, ordres de grandeurs, interprétation des courbes, intérêt d'un tableur, rentabilité d'une opération, consommations électriques, coordonnées GPS, etc.)
- Comprendre comment développer des réflexes de calculs courants dans le monde professionnel, notamment dans la gestion, les finances, les statistiques, le BTP, l'architecture et l'ingénierie.
Elle s'adresse donc à tous : La simple connaissance des tables de multiplication suffit !
Les sujets suivants sont ainsi abordés de manière progressive, toujours illustrés d'exemples :
- Règles générales de calculs (multiples, puissances, arrondis, etc.).
- Systèmes d'unités (distances, poids, température, temps, binaire, etc.) avec conversions courantes (miles-kilomètres).
- Intérêt des fractions/pourcentages (calcul de proportions, taux, ratios, règle de trois, redimensionnement d'une image, etc.).
- Statistiques, avec exemples en économie (PIB, INSEE, etc.).
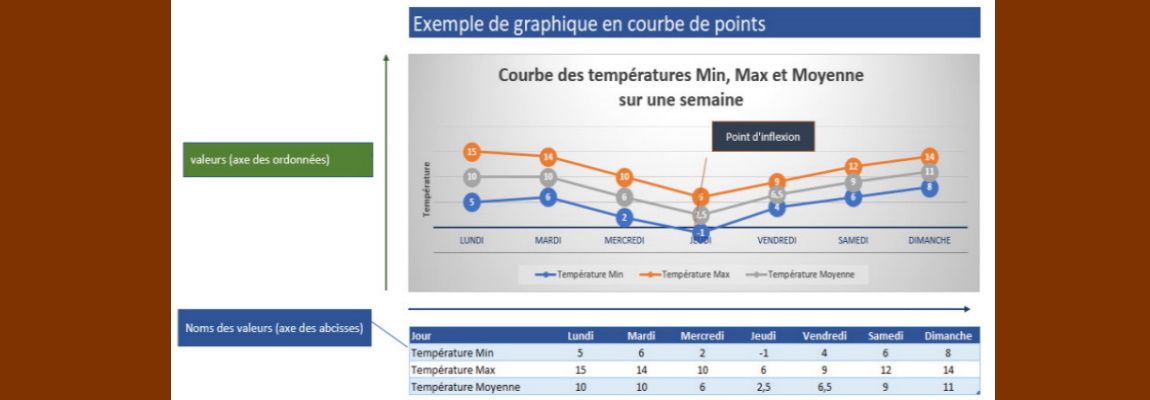
- Principe et intérêt d'un graphique.
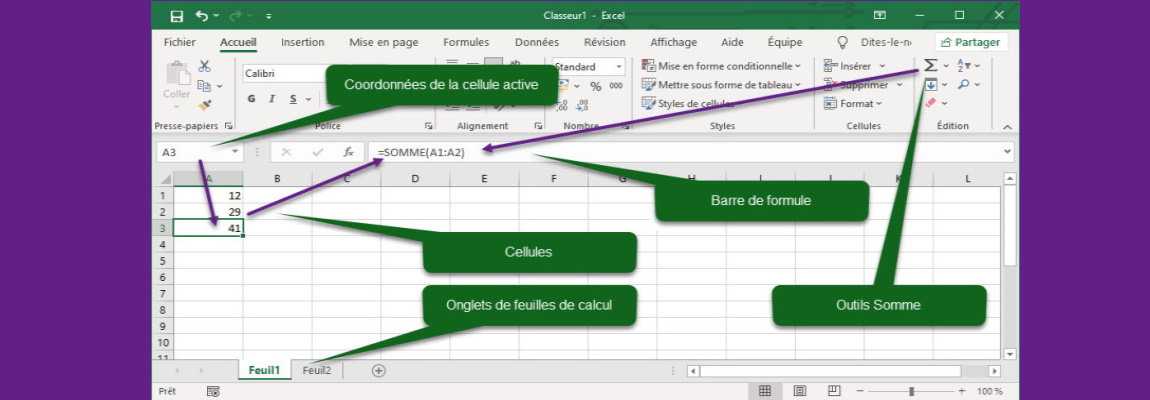
- Principe et intérêt d'un tableur de type Excel.
- Règle des calcul avec les formes géométriques courantes (proportions et nombre d'or).
- Système de coordonnées Euclidien X,Y pour tracer des formes 2D.
- Intérêt et mise en pratique de la trigonométrie (calcul de distances).
- Applications en physique : calcul de vitesse, puissances électriques avec ordres de grandeur pour comprendre
les différents niveaux de consommation (maison, ville, pays). - Système de coordonnées GPS.
- Les grands noms de l'histoire des sciences et leurs découvertes (Thalès, Pythagore, Aristote, Galilée, Léonard de Vinci, Kepler, Newton, Maxwell, Einstein, Poincarré, John von Neumann, Turing, ...).
Objectifs par niveaux scolaire
Bien que l'approche pédagogique proposée ne soit pas scolaire, une grande partie des règles de calcul présentées ici correspondent à des sujets abordés de la 6ème à la terminale. En voici la liste, avec les exemples d'applications correspondant :
6ème
- Nombres décimaux (réels)
- Calculs simples (multiplication et quotien (division de nombre entiers).
- Systèmes d'unités (distances, poids, température, temps) avec ordres de grandeur.
- Formes géométriques courantes (cercles, ellipses, rectangles, parallélogrammes, triangles).
- Calcul de périmètres, de surfaces et de volumes.
5ème
- Règles de priorité entres les opérateurs arithmétiques.
- Les fractions avec mise en pratique pour calculer des proportions.
- Principe et intérêt d'un tableur de type Excel.
- Règle des calcul avec les formes géométriques courantes.
- Intérêt et mise en pratique de la trigonométrie (calcul de distances).
4ème
- Critères de divisibilité.
- Puissances et racine carrée.
- Notation scientifique des nombres.
- Produits en croix (mise en application application avec la règle de trois).
- Principe et intérêt d'un graphique.
- Principe et intérêt d'un tableur.
- Choix d'une échelle de grandeur.
- Pourcentages (mise en application avec calcul de ratios).
- Statistiques courantes, avec exemples en économie (PIB, ratios par secteurs, etc.).
3ème
- Nombres premiers avec exemple d'applications en sécurité informatique.
- Puissances, avec règles de calculs de multiplications/division par 10.
- Triangles rectangles avec règles de calcul de distances.
- Intérêt et mise en pratique de la trigonométrie (calcul de distances).
Seconde
- Nombres irrationnels.
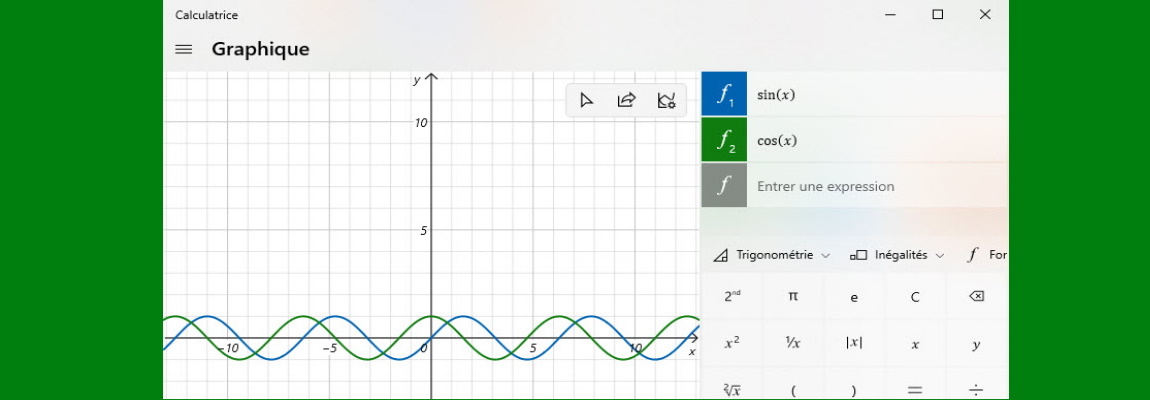
- Fonctions (croissance, représentation en courbe avec la calculatrice de Windows).
Première
- Suites et séries, avec mise en application pour le calcul de PI.
Terminale
- Trigonométrie : fonctions Sinus, Cosinus, Tangente avec mise en application pour le calcul de distances.